Data Analysis using Regression and Multilevel Models is one of the books I liked. I think it is a different book on Regression Models, one that focus on the modeling part more than in the mathematical part. I mean, it is for sure important to have the mathematical foundation, even more so now with all these Bayesian models coming around. But when using regression for causal inference, I feel that for most part the lack of modeling expertise rather than mathematical expertize is what drives the low quality of many works. I am reading the book for the second time and I will leave some points I think is important here.
Chapter 3 is about the basics of regression models. It does a good job talking about basic things, like binary predictors and interactions, also using scaterplots to make things visual. These are some points I would like to flag:
1 - Think about the intercept as the point where X is zero, this has always helped me interpret it. Sometimes X =0 will not make much sense and then centralizing the predictor might help.
2 - One can interpret the regression in a predictive or counterfactual way. The predictive interpretation focus on group comparison, sort of exploring the world out there, what is the difference between folks with X =0 and folks with X =1. The counterfactual interpretation is more about effects of changing X by one unit. If we increase X by one unit how the world out there will change. This is as I see the difference between modeling and not fitting a model.
3 - Interactions should be included in the model when main effects are large. When using binary variables interactions are a way of fitting different models to different groups.
4 - Always look at the residual versus the predicted as a diagnostic.
5 - Use graphics to display precision of coefficients. Use the R function "sim" for simulations.
6 - Make sure regression is the right tool to use and that the variables you are using are the correct ones to answer your research question. The validity of the Regression Model for the research question is put by the book as the most important assumption of the regression model.
7 Additivity and Linearity is the second most important assumption. Use transformation on the predictors if these assumptions are not matched.
8 - Normality and equal variance are less important assumption.
9 - The best way to validate a model is to test it in the real world, with a new set of data. A model is good when it can be replicated with external data.
For those who likes R, the book has plenty of codes that can be used by the beginners as a starting point for learning the software.
Sunday, 19 December 2010
Saturday, 11 December 2010
Which model?
It happened just last month, a paper of ours submitted to a journal got rejected mainly because of many non methodological problems, but there was one critic related to our regression model. Since our dependent variable was a sort of count, we were asked to explain why using a linear regression model instead of a Poisson model.
We noticed the highly skewed nature of the dependent variable, so we applied the logarithmic transformation before fitting the linear model. To make coefficients more easily interpretable we exponentiated them and presented the results with confidence intervals.
Upon receiving the comment from the publisher reviewer, we decided to go back and readjust the data using the Poisson model. It turned out that the Poisson model was not adequate because of overdispersion, so we fitted the Negative Binomial model instead, with log link. It worked nicely but for our surprise the coefficients were nearly identical to the ones from the linear model, fitted with logarithmic transformation of the dependent variable.
It feels good when you do the right thing and you can say "I used a Negative Binomial Model", it looks like you are a professional statistician using high level and advanced models, the state of art type of thing, despite of the fact that this model is around for quite some time and what makes it to look good is, perhaps, the fact that the linear regression model is by far almost the only think know outside of statistical circles.
But my point is that to me it is not really clear how worth is to go to the Negative Binomial model when conclusions will not be different from the simpler linear model. Maybe it makes sense to take the effort to go the most advanced way in a scientific paper, but we also have the world out there where we need to be pragmatic. Does it pay to use the Poisson, Negative Binomial, Gamma or whatever model in the real world or it ends up being just academic distraction? Maybe in some cases it does pay out, like if you think about some financial predictive models out there, but for most part my impression is that we do not add value by using more advanced and technically correct statistical methods. This might seem a word against statistic but I think it is the opposite. We, as statistician, should pursue the answer to questions like this, so to know when it is important seeking more advanced methods and when we might do just as well with simple models...
We noticed the highly skewed nature of the dependent variable, so we applied the logarithmic transformation before fitting the linear model. To make coefficients more easily interpretable we exponentiated them and presented the results with confidence intervals.
Upon receiving the comment from the publisher reviewer, we decided to go back and readjust the data using the Poisson model. It turned out that the Poisson model was not adequate because of overdispersion, so we fitted the Negative Binomial model instead, with log link. It worked nicely but for our surprise the coefficients were nearly identical to the ones from the linear model, fitted with logarithmic transformation of the dependent variable.
It feels good when you do the right thing and you can say "I used a Negative Binomial Model", it looks like you are a professional statistician using high level and advanced models, the state of art type of thing, despite of the fact that this model is around for quite some time and what makes it to look good is, perhaps, the fact that the linear regression model is by far almost the only think know outside of statistical circles.
But my point is that to me it is not really clear how worth is to go to the Negative Binomial model when conclusions will not be different from the simpler linear model. Maybe it makes sense to take the effort to go the most advanced way in a scientific paper, but we also have the world out there where we need to be pragmatic. Does it pay to use the Poisson, Negative Binomial, Gamma or whatever model in the real world or it ends up being just academic distraction? Maybe in some cases it does pay out, like if you think about some financial predictive models out there, but for most part my impression is that we do not add value by using more advanced and technically correct statistical methods. This might seem a word against statistic but I think it is the opposite. We, as statistician, should pursue the answer to questions like this, so to know when it is important seeking more advanced methods and when we might do just as well with simple models...
Crowd Estimates
It appeared in the last Chance News a short article about the challenges of estimating the number of persons in a crowd. I haven't seen much about crowd estimates in the statistical literature, but it looks like by far the most acceptable way of estimating a crowd is by aerial photos. By using estimates of the density (persons per area) one can get to an estimate of the size of the crowd.
One problem with aerial photos is that it captures a moment and therefore will make it possible to estimate the crowd at that specific moment. If you arrived at the place before the photo and left the place before the photo, you are not included in the picture. I can see that that is okay for gatherings like the Obama's swearing, or any sort of event that is composed of a single moment, like a speech. But if you think about events that go over a period of time, like the Carnival in Brazil or the Caribana in Toronto then you need more than photos, and even photos taken at different points in time can be problematic because you don't know the amount of folks that are in, say, two photos.
Sometime ago I got involved in a discussion about how to estimate the number of attendees in the Caribana Festival. This is a good challenge, one that I am not sure can be accomplished with good accuracy. We thought about some ways to get this number.
The most precise way, I think all agreed, would be by conducting two surveys. One in the event to estimate the percentage of participants that were from Toronto. This by itself is not a simple thing in terms of sampling design if you think that the Caribana goes over 2 or 3 days, in different locations. But lets not worry about the sampling here (maybe in another post). The other survey would be among Torontonians, to estimate what is the percentage of the folks living in the city that went to the event. Because we have good estimates of the Toronto population, this survey will give us the estimate of the number of Torontonians that went to the event. From the first survey we know that they are X percent of the total, so we can estimate the total attendance to the event.
Another way, we thought, would be to spread some sort of thing to the crowd. For example, we could distribute a flier to the crowd. This should be done randomly. Then we, also with a random sample, interview folks in the crowd and ask then whether or not they received the flier. By knowing the percentage of the crowd that received the fliers and the total number of fliers distributed we can also get to an estimate of the crowd.
A related way would be by measuring the consumption of something. We thought about cans of coke. If we could get a good estimate of the number of cans of coke sold in the area and if we could conduct a survey to estimate the percentage of the crowd that bought a can of coke (or average number of cans per person) we could then sort out the crowd size.
Another way would be to use external information about garbage. It is possible to find estimates of the average amount of garbage produced by an individual in a crowd. The if you work with the garbage collectors to weight the garbage from the event, you could get to an estimate of the crowd. A problem with an external estimate of something like amount of garbage per person is that it could variate a lot depending on the event, the temperature, weather, place, availability of food and drinks and so on. So I am not sure this method would work very well, maybe some procedure could be put in place to follow a sample of attendees (or maybe just interview them) to get an estimate amount of garbage generated per person.
Finally, an aerial photo could be combined with a survey in the ground. Photos could be taken in different points in time and a survey would ask participants when they arrived at the event and when they intend to leave. Of course the time one leaves the event will not be very accurately estimated but hopefully things would cancel out and in average we would be able to estimate the percentage of the crowd that are in two consecutive photos, so that we can account for that in the estimation.
I think crowd estimates is an area not much developed for these events that goes for a long period of time. There is room for creative and yet technically sound approaches.
One problem with aerial photos is that it captures a moment and therefore will make it possible to estimate the crowd at that specific moment. If you arrived at the place before the photo and left the place before the photo, you are not included in the picture. I can see that that is okay for gatherings like the Obama's swearing, or any sort of event that is composed of a single moment, like a speech. But if you think about events that go over a period of time, like the Carnival in Brazil or the Caribana in Toronto then you need more than photos, and even photos taken at different points in time can be problematic because you don't know the amount of folks that are in, say, two photos.
Sometime ago I got involved in a discussion about how to estimate the number of attendees in the Caribana Festival. This is a good challenge, one that I am not sure can be accomplished with good accuracy. We thought about some ways to get this number.
The most precise way, I think all agreed, would be by conducting two surveys. One in the event to estimate the percentage of participants that were from Toronto. This by itself is not a simple thing in terms of sampling design if you think that the Caribana goes over 2 or 3 days, in different locations. But lets not worry about the sampling here (maybe in another post). The other survey would be among Torontonians, to estimate what is the percentage of the folks living in the city that went to the event. Because we have good estimates of the Toronto population, this survey will give us the estimate of the number of Torontonians that went to the event. From the first survey we know that they are X percent of the total, so we can estimate the total attendance to the event.
Another way, we thought, would be to spread some sort of thing to the crowd. For example, we could distribute a flier to the crowd. This should be done randomly. Then we, also with a random sample, interview folks in the crowd and ask then whether or not they received the flier. By knowing the percentage of the crowd that received the fliers and the total number of fliers distributed we can also get to an estimate of the crowd.
A related way would be by measuring the consumption of something. We thought about cans of coke. If we could get a good estimate of the number of cans of coke sold in the area and if we could conduct a survey to estimate the percentage of the crowd that bought a can of coke (or average number of cans per person) we could then sort out the crowd size.
Another way would be to use external information about garbage. It is possible to find estimates of the average amount of garbage produced by an individual in a crowd. The if you work with the garbage collectors to weight the garbage from the event, you could get to an estimate of the crowd. A problem with an external estimate of something like amount of garbage per person is that it could variate a lot depending on the event, the temperature, weather, place, availability of food and drinks and so on. So I am not sure this method would work very well, maybe some procedure could be put in place to follow a sample of attendees (or maybe just interview them) to get an estimate amount of garbage generated per person.
Finally, an aerial photo could be combined with a survey in the ground. Photos could be taken in different points in time and a survey would ask participants when they arrived at the event and when they intend to leave. Of course the time one leaves the event will not be very accurately estimated but hopefully things would cancel out and in average we would be able to estimate the percentage of the crowd that are in two consecutive photos, so that we can account for that in the estimation.
I think crowd estimates is an area not much developed for these events that goes for a long period of time. There is room for creative and yet technically sound approaches.
Sunday, 5 December 2010
The science of status
For quite some time now I have been concerned with the quality of the science that we see in journals in fields like Medicine and Biology. Statistics play a fundamental role in the experimental method necessary for the development of much of human science, but what we see is the science of publishing rather that the science of evidence. Statistical Inference has been disseminated as tool for getting your paper published rather that making science. A as result the bad use of statistics in papers that offer not replicable results are widespread. Here is an interesting paper about the subject.
Unfortunately not only the scientific research lose with the low quality of research and misuse of statistics. The Statistics itself lose by being distrusted as a whole for many people that end up considering the statistical method as faulty and not appropriated when its use by not proficient researchers is to blame.
What is our role as statisticians? We need to do the right thing. We should not be blinded by the easy status that comes with our name in a paper after running a regression analysis. We need to be more than softwares pilots that press buttons for those own the data. We need to question, to understand the problem and to make sure the regression is the right thing to do. If we don't remember the regression class we need to go back and refresh our memory before using statistical models. We need to start ding the right thing and knowing what we are doing. Then we need to pursue and criticize the publications that use faulty statistics because we are among the few who can identify faulty statistics. For the most part the researchers run models that they don't understand and get away with it because nobody else understand it as well.
But often we are among them, we are pleased with our name in publications, and we are happy to go the easiest way.
I decided to write this after a quick argument in a virtual community of statistician, where I noticed a well quoted statistician spreading the wrong definition o p-value. We can't afford to have this kind of thing inside our own community, we need to know what is a p-value...
Unfortunately not only the scientific research lose with the low quality of research and misuse of statistics. The Statistics itself lose by being distrusted as a whole for many people that end up considering the statistical method as faulty and not appropriated when its use by not proficient researchers is to blame.
What is our role as statisticians? We need to do the right thing. We should not be blinded by the easy status that comes with our name in a paper after running a regression analysis. We need to be more than softwares pilots that press buttons for those own the data. We need to question, to understand the problem and to make sure the regression is the right thing to do. If we don't remember the regression class we need to go back and refresh our memory before using statistical models. We need to start ding the right thing and knowing what we are doing. Then we need to pursue and criticize the publications that use faulty statistics because we are among the few who can identify faulty statistics. For the most part the researchers run models that they don't understand and get away with it because nobody else understand it as well.
But often we are among them, we are pleased with our name in publications, and we are happy to go the easiest way.
I decided to write this after a quick argument in a virtual community of statistician, where I noticed a well quoted statistician spreading the wrong definition o p-value. We can't afford to have this kind of thing inside our own community, we need to know what is a p-value...
Saturday, 6 November 2010
Data visualization
We are always challenged to extract useful information from data. This involves also presenting this information in a way that people can understand it. And no doubt that the easiest way of making sense of numbers is by seeing them in chart. The technology evolves everyday and with it new and creative data visualization tools comes up.
This site links to a video that attracted my attention as a good resource for data visualization. If you watch the videos you will see many creative ways of presenting the information and hear from the trends we are facing in terms of data visualization.
I am not by any means an expert on this subject but I cannot ignore it as to me this is what the future is going to be about. But with the ease of creating graphs and visualizing data comes also a concern - The attraction of the visual tools should not override the quality of the information. We have seen many instances where information is not clear if not misleading and I think there should have more criteria on how information are shown to the general public that as a rule don't have training on interpreting data.
This is an example of data visualization mentioned in the above video that can be very attractive at first sight but penalizes the interpretation of the information. The movie also talks about BBC News and its approach toward more modern data visualization. Here you have an example graphs in their website. I was exploring it. If you click the tabs "In Graphics" and then "Weather" a pie chart appears showing that most of the deaths on the roads happens when the weather is "Fine". What does that mean? It can mean different things or nothing. I have an idea of British as a country with grey skies (overcast) perhaps because I've heard many times about the not so nice weather. So if the weather is not usually fine and still the majority of deaths happens with fine weather, that means that fine weather is associated with deaths on the roads. Maybe people speed more because the weather is good. But maybe the impression I have is not correct and the weather is fine most of the time and if so I would expect most of the deaths to happen with fine weather if there is not association of death and weather. So, without knowing the distribution of the weather it is impossible to extract useful information from this graph. We know that deaths happens with fine weather but we don't know whether or not there is an association between deaths and weather. It becomes a very superficial analysis.
We can understand this point easily if we look at the "Sex" tab. Notice that the majority of deaths are males. We know that the distribution of gender should be close to 1:1, so we can say that males are much more at risk than females, or in other words, there is an association between deaths and gender. And we can start thinking on why this happens (is it because males are less careful when driving?) and here we enter the difficult field of causal analysis in statistics. In the "Weather" tab we cannot get to this point because we don't even know if there is an association.
I am ok with data visualization and new advanced tools for this, but it concerns me at the same time that these technology becomes available and easily used by anyone at their will. I do not favor the strict control of the use of such tools - like, only statistician can do advanced graphics or publish them - but I start to think that some kind of control should be in place for the information released to the public, as it is for food, for example. Of course in the age of the internet this seems utopia but is nonetheless a concern.
It is amazing the amount of data already available online, meaning that one does not need to have data to play with data visualization tools. I want to finish this post with a link to Google public data, which make available data and tools to chart them. You can play a lot there. I want to finish with a multiple time series I created, comparing countries according to their CO2 emission. I have always been impressed on how Canadians are so much more environmentally concerned than Brazilians. But at the same time they drive bigger cars and live in bigger houses. So I was curious to see which country "damages" more the environment through CO2 emission. It is impressive how Canada is ahead of Brazil despite of Brazilian population being more than 6 times larger. It is easy to fight for the environment if you are not starving, have a big car in the garage and a house 5 times bigger than what you need...
This site links to a video that attracted my attention as a good resource for data visualization. If you watch the videos you will see many creative ways of presenting the information and hear from the trends we are facing in terms of data visualization.
I am not by any means an expert on this subject but I cannot ignore it as to me this is what the future is going to be about. But with the ease of creating graphs and visualizing data comes also a concern - The attraction of the visual tools should not override the quality of the information. We have seen many instances where information is not clear if not misleading and I think there should have more criteria on how information are shown to the general public that as a rule don't have training on interpreting data.
This is an example of data visualization mentioned in the above video that can be very attractive at first sight but penalizes the interpretation of the information. The movie also talks about BBC News and its approach toward more modern data visualization. Here you have an example graphs in their website. I was exploring it. If you click the tabs "In Graphics" and then "Weather" a pie chart appears showing that most of the deaths on the roads happens when the weather is "Fine". What does that mean? It can mean different things or nothing. I have an idea of British as a country with grey skies (overcast) perhaps because I've heard many times about the not so nice weather. So if the weather is not usually fine and still the majority of deaths happens with fine weather, that means that fine weather is associated with deaths on the roads. Maybe people speed more because the weather is good. But maybe the impression I have is not correct and the weather is fine most of the time and if so I would expect most of the deaths to happen with fine weather if there is not association of death and weather. So, without knowing the distribution of the weather it is impossible to extract useful information from this graph. We know that deaths happens with fine weather but we don't know whether or not there is an association between deaths and weather. It becomes a very superficial analysis.
We can understand this point easily if we look at the "Sex" tab. Notice that the majority of deaths are males. We know that the distribution of gender should be close to 1:1, so we can say that males are much more at risk than females, or in other words, there is an association between deaths and gender. And we can start thinking on why this happens (is it because males are less careful when driving?) and here we enter the difficult field of causal analysis in statistics. In the "Weather" tab we cannot get to this point because we don't even know if there is an association.
I am ok with data visualization and new advanced tools for this, but it concerns me at the same time that these technology becomes available and easily used by anyone at their will. I do not favor the strict control of the use of such tools - like, only statistician can do advanced graphics or publish them - but I start to think that some kind of control should be in place for the information released to the public, as it is for food, for example. Of course in the age of the internet this seems utopia but is nonetheless a concern.
It is amazing the amount of data already available online, meaning that one does not need to have data to play with data visualization tools. I want to finish this post with a link to Google public data, which make available data and tools to chart them. You can play a lot there. I want to finish with a multiple time series I created, comparing countries according to their CO2 emission. I have always been impressed on how Canadians are so much more environmentally concerned than Brazilians. But at the same time they drive bigger cars and live in bigger houses. So I was curious to see which country "damages" more the environment through CO2 emission. It is impressive how Canada is ahead of Brazil despite of Brazilian population being more than 6 times larger. It is easy to fight for the environment if you are not starving, have a big car in the garage and a house 5 times bigger than what you need...
Sunday, 24 October 2010
Trends
The new edition of the Journal of Official Statistics has just been released. The first paper is by Sharon Lohr, author of the well known sampling book Sampling: Design and Analysis which I still did not read to tell the truth. The paper is not technical, it is rather an article that surveys the program currently offered in courses of statistics in US and how statisticians should learn sampling theory.
I knew that sampling is not a course highly rated in importance in Universities in Brazil and I did not expect it to be different in US. I am familiar with the difficulties encountered on finding a professor that is willing to advise you if you want to do a master or phD related to sampling theory. All that contradicts the importance that sampling has in our (statisticians) day to day work and I think that the consequences are that many of us overlook the sampling part of whichever data we are analyzing. But that is not really the point I want to talk about here.
Back in the 80s, when I did not even knew what statistics was all about, I had an excellent literature teacher who once said "The history of literature is made of trends. A period is characterized by rational literature, the next is subjective, emotional, the next is rational again and so on until the current period...". Well, I am not sure this was exactly what she said since it was a long time ago, but Lohr's paper made me think about these interchanges in the context of sampling.
Before the 1930's sampling was done only by convenience. Then probabilistic sample theory was introduced under lots of skepticism. It was really hard to believe a random sample could give better results than a convenience sample. How would a random sample make sure not everybody in the sample supports one candidate? Or the correct age distribution? Lrhs says the book Sample Survey Methods and Theory by Hansen, Hurwitz, and Madow (1953) had a great influence on the introduction of probability sampling in practical work. The book (actually two volumes) is well coted still today and is in my wish list.
I guess we can say probability sampling dominated the sampling theory and its practice until a while ago, when the internet came into play. As for now the internet is not suitable for probability samples but despite of that its ease and cheapness has overtaken the reliability offered be the sampling theory. Definitely internet based sampling is taking us back to the convenience sampling, which does not necessarily means that we are going backwards. The challenge to me is to adapt ourselves to the new reality.
We still have many statisticians putting themselves against non probabilistic sample. But what are the instances where we can have a truly probability sample if the target are human beings? Even official institutions, that have a good budgets to spend on sampling, have trouble with high non response rates. In the business world the probability sample has rarely happened and it might become even worst. Still surveys are more and more popular. In the business world you just don't have work if you refuses to work with non probability samples. We need to understand how to get more reliable results from internet surveys, how build models that correct possible biases, how to interpret and release results for which precision is hard to grasp without misleading the user of the information. I think right now we are doing a very poor job on this regard, at least most of us, because the lack of theory and knowledge about non probability sampling has lead to the use of probability sampling theory for non probability sample. The assumptions needed for this practice is rarely understood.
We are in a new age where so much information are available online and at so low cost. We just cant afford to ignore it because it comes from methods not recognized by statistical theory, rather we need to accept the challenge of making the information useful.
I knew that sampling is not a course highly rated in importance in Universities in Brazil and I did not expect it to be different in US. I am familiar with the difficulties encountered on finding a professor that is willing to advise you if you want to do a master or phD related to sampling theory. All that contradicts the importance that sampling has in our (statisticians) day to day work and I think that the consequences are that many of us overlook the sampling part of whichever data we are analyzing. But that is not really the point I want to talk about here.
Back in the 80s, when I did not even knew what statistics was all about, I had an excellent literature teacher who once said "The history of literature is made of trends. A period is characterized by rational literature, the next is subjective, emotional, the next is rational again and so on until the current period...". Well, I am not sure this was exactly what she said since it was a long time ago, but Lohr's paper made me think about these interchanges in the context of sampling.
Before the 1930's sampling was done only by convenience. Then probabilistic sample theory was introduced under lots of skepticism. It was really hard to believe a random sample could give better results than a convenience sample. How would a random sample make sure not everybody in the sample supports one candidate? Or the correct age distribution? Lrhs says the book Sample Survey Methods and Theory by Hansen, Hurwitz, and Madow (1953) had a great influence on the introduction of probability sampling in practical work. The book (actually two volumes) is well coted still today and is in my wish list.
I guess we can say probability sampling dominated the sampling theory and its practice until a while ago, when the internet came into play. As for now the internet is not suitable for probability samples but despite of that its ease and cheapness has overtaken the reliability offered be the sampling theory. Definitely internet based sampling is taking us back to the convenience sampling, which does not necessarily means that we are going backwards. The challenge to me is to adapt ourselves to the new reality.
We still have many statisticians putting themselves against non probabilistic sample. But what are the instances where we can have a truly probability sample if the target are human beings? Even official institutions, that have a good budgets to spend on sampling, have trouble with high non response rates. In the business world the probability sample has rarely happened and it might become even worst. Still surveys are more and more popular. In the business world you just don't have work if you refuses to work with non probability samples. We need to understand how to get more reliable results from internet surveys, how build models that correct possible biases, how to interpret and release results for which precision is hard to grasp without misleading the user of the information. I think right now we are doing a very poor job on this regard, at least most of us, because the lack of theory and knowledge about non probability sampling has lead to the use of probability sampling theory for non probability sample. The assumptions needed for this practice is rarely understood.
We are in a new age where so much information are available online and at so low cost. We just cant afford to ignore it because it comes from methods not recognized by statistical theory, rather we need to accept the challenge of making the information useful.
Sunday, 12 September 2010
Multiple Sclerosis and Statistics
Yesterday I was listening to a program on CBC Radio about a new treatment for Multiple Sclerosis. The program is indeed very interesting and exposes the widespread problem of non scientific news in the scientific world.
The new treatment for Multiple Sclerosis conducted by the Italian Doctor Zamboni has gained considerable space in the media and this is not the first time I hear about it. While there are some people saying that they got substantial improvement through the treatment, the public health system in Canada refuses to conduct the procedure under the allegation that it is not scientifically tested and proved to be efficient. This obligates those who believe in the treatment to seek it outside of the country and at the same time it brings a bad image for the Canadian Health System since it seems that it is not giving an opportunity of a better life to many Canadians.
I agree that in a public system that has shortage of resources we should avoid spending money with procedures unproven to be of any effect. But if there are evidences of positives effects then I think a good system would test the procedure on scientific grounds as soon as possible. But I would like to talk a little bit about the statistical part of this problem, one which the overall population is usually not aware of.
Suppose that 10 individuals with Multiple Sclerosis submit themselves to the new procedure under a non scientific environment (they just get the procedure without being in a controlled experiment) and one of them has some improvement. What usually happens is that there is a biased coverage of the 10 results by the media. 9 folks go home with no improvement and nobody talk about them while the one that had benefits becomes very happy and talk to everybody and the media interview the guy reporting perhaps that a new cure has been found. Now everybody with MS will watch the news and look for the procedure.
This is just one side of the absence of a designed scientific experiment. Others consequences at least as important are 1) the possibility that the improvement is just a short term one and things could even get worse after some time and 2) the possibility that we are looking at what is called placebo effect. Placebo Effect is the improvement in health conditions due to some reason other than the procedure. Sometimes just the fact that the somebody thinks he/she is receiving a miraculous treatment will cause some improvement.
We cannot say that the procedure is innocuous at the present moment. The right thing to do would be to conduct a controlled experiment as soon as possible so that if results are positive the maximum number of people can benefit from it. It is also important that the experiment be conducted in more than one place because only different instances with positive result can definitely validate the efficacy of the treatment. Fortunately it looks like trials have started in both US and Canada.
As for now it is quite hard to quantify the real effects of the treatment and we have to recognize that those who are facing MS have a difficult decision to make, even those who understand perfectly the possible inefficacy of this procedure. Without being able to assess the risks, should somebody with MS look for the treatment or wait until long lasting clinical trials results come along? I guess this will depend on the specific case, but it is a hard decision anyway....
The new treatment for Multiple Sclerosis conducted by the Italian Doctor Zamboni has gained considerable space in the media and this is not the first time I hear about it. While there are some people saying that they got substantial improvement through the treatment, the public health system in Canada refuses to conduct the procedure under the allegation that it is not scientifically tested and proved to be efficient. This obligates those who believe in the treatment to seek it outside of the country and at the same time it brings a bad image for the Canadian Health System since it seems that it is not giving an opportunity of a better life to many Canadians.
I agree that in a public system that has shortage of resources we should avoid spending money with procedures unproven to be of any effect. But if there are evidences of positives effects then I think a good system would test the procedure on scientific grounds as soon as possible. But I would like to talk a little bit about the statistical part of this problem, one which the overall population is usually not aware of.
Suppose that 10 individuals with Multiple Sclerosis submit themselves to the new procedure under a non scientific environment (they just get the procedure without being in a controlled experiment) and one of them has some improvement. What usually happens is that there is a biased coverage of the 10 results by the media. 9 folks go home with no improvement and nobody talk about them while the one that had benefits becomes very happy and talk to everybody and the media interview the guy reporting perhaps that a new cure has been found. Now everybody with MS will watch the news and look for the procedure.
This is just one side of the absence of a designed scientific experiment. Others consequences at least as important are 1) the possibility that the improvement is just a short term one and things could even get worse after some time and 2) the possibility that we are looking at what is called placebo effect. Placebo Effect is the improvement in health conditions due to some reason other than the procedure. Sometimes just the fact that the somebody thinks he/she is receiving a miraculous treatment will cause some improvement.
We cannot say that the procedure is innocuous at the present moment. The right thing to do would be to conduct a controlled experiment as soon as possible so that if results are positive the maximum number of people can benefit from it. It is also important that the experiment be conducted in more than one place because only different instances with positive result can definitely validate the efficacy of the treatment. Fortunately it looks like trials have started in both US and Canada.
As for now it is quite hard to quantify the real effects of the treatment and we have to recognize that those who are facing MS have a difficult decision to make, even those who understand perfectly the possible inefficacy of this procedure. Without being able to assess the risks, should somebody with MS look for the treatment or wait until long lasting clinical trials results come along? I guess this will depend on the specific case, but it is a hard decision anyway....
Friday, 10 September 2010
Respondent Driven Sampling
I just read this paper: Assessing Respondent-driven Sampling, published on the Proceedings of the National Academy of Sciences. The problem of measuring traits in rare population has always been a shortcoming of existing sampling method, when we think about practical applications.
I faced the challenge once, when I had to design a sample of homeless people in a very large city. But rather than talk about this specific work, I prefer to use it here as an example to show some problems we have with this type of challenge.
If you wanted to estimate the size of the homeless populations by means of a traditional sample, you would need to draw a quite large probabilistic sample to get some few homeless folks who will allow you to project results to the entire homeless population. The first problem with this is to make sure your sample frame cover the homeless population, because it will likely not. Usually samples that covers the human population of a country is ironically based on households (and we are talking about homeless people) and the nice fact the official institutes like Statistics Canada can give you household counts for small areas, which can then become units in your sample frame. Well, perhaps you can somehow include in your sample frame homeless people by looking for them in the selected areas and weighting afterwards... but I just want to make the point that we have already started with a difficult task even if we could draws a big probabilistic sample. Then I want to move on.
Usually estimating the size of rare population is only the least important of a list of goals a researcher has. The second goal would be to have a good sample of the targeted rare population so that we can draw inferences that are specific for that population. For example, we could be interested in the proportion of homeless people with some sort of mental disorder. This requires a large enough sample of homeless people.
One way to get a large sample of homeless people would be by referrals. It is fair to assume that the members of this specific rare population know other. Once we get one of them, they can indicate others in a process widely known as Snowball Sampling. Before the mentioned paper I was familiar with the term and just considered it as another type of Convenience Sampling for which inference always depends on strong assumption linked to the non probabilistic nature of the sample. But there are some literature on the subject and moreover, it seems to be more widely used than I thought.
Respondent Driven Sampling (RDS) seems to be the most modern way of reaching hidden populations. In a RDS an initial sample is selected and those sampled subjects receive incentive to bring their peers who also belongs to the given population hidden. They get incentives if they answer the survey and if they successfully bring others subjects. RDS would be different from the Snowball Sample because the later ask subjects to name their peers, not to bring them over to the research site. This is an interesting paper to learn more about it.
Other sampling methods include Targeted Sampling where the research tries to make a preliminary list of eligible subjects and sample from there. Of course this is usually not very helpful because of costs and again the difficulty to reach some rare population. Key Informant Sampling is a sample where you would select, for example, people that work with the target population. They would give you information about the population, that is, you would not really sample subjects from the population, but instead would make your inferences through secondary sources of information. Time Space Sampling (TTS) is method where you list places and within those places, times when the target population can be reach. For example, a list of public eating places could be used to find homeless people and you know what time they can be reach. It is possible to have valid inferences for the population that goes to these places by sampling places and times interval in this list. You can see more about TTS sampling and find other references in this paper.
Now to a point about the paper I first mentioned, how good is RDS Sampling? Unfortunately the paper does not brings good news. According to the simulations they did, the variability of the RDS sample is quite high, with median design effect around 10. That means a RDS sample of size n would be as efficient (if we think about Margin of Error) as a Simple Random Sample of size n/10. That makes me start questioning the research, although the authors make good and valid points defending the assumptions they need to make so that their simulations becomes comparable to a real RDS. I don't know, I cannot say anything, but I wonder if out there a survey exist that has used RDS sample for several consecutive waves. I think this kind of survey would give us some ideas of the variability involved on replications of the survey. Maybe we could look at some traits that are not expected to change from wave to wave and make an assessment of its variability.
An interesting property of the RDS is that it tends to lose it bias with time. For example, it was noticed that if a black person is asked for referrals, the referrals tend to be more black the actual proportion of black people in the population. This seems to me a natural thing in networks, I mean, people tend to have peers that are similar to themselves. This will happen with some (or maybe most) of the demographics characteristics. But it looks like the evident bias present in the first wave of referrals seemingly disappear around the sixth wave. That seems to me to be a good thing and if the initial sample cannot be random maybe we should consider disregarding waves 1 to 5 or so.
Anyway, I think as of today researches still face huge technical challenges when the target population is rare. RDS and other methods of reaching these populations have been developed which helps a lot, but this remains an unresolved issue for statistician, one very important in sampling methodology.
I faced the challenge once, when I had to design a sample of homeless people in a very large city. But rather than talk about this specific work, I prefer to use it here as an example to show some problems we have with this type of challenge.
If you wanted to estimate the size of the homeless populations by means of a traditional sample, you would need to draw a quite large probabilistic sample to get some few homeless folks who will allow you to project results to the entire homeless population. The first problem with this is to make sure your sample frame cover the homeless population, because it will likely not. Usually samples that covers the human population of a country is ironically based on households (and we are talking about homeless people) and the nice fact the official institutes like Statistics Canada can give you household counts for small areas, which can then become units in your sample frame. Well, perhaps you can somehow include in your sample frame homeless people by looking for them in the selected areas and weighting afterwards... but I just want to make the point that we have already started with a difficult task even if we could draws a big probabilistic sample. Then I want to move on.
Usually estimating the size of rare population is only the least important of a list of goals a researcher has. The second goal would be to have a good sample of the targeted rare population so that we can draw inferences that are specific for that population. For example, we could be interested in the proportion of homeless people with some sort of mental disorder. This requires a large enough sample of homeless people.
One way to get a large sample of homeless people would be by referrals. It is fair to assume that the members of this specific rare population know other. Once we get one of them, they can indicate others in a process widely known as Snowball Sampling. Before the mentioned paper I was familiar with the term and just considered it as another type of Convenience Sampling for which inference always depends on strong assumption linked to the non probabilistic nature of the sample. But there are some literature on the subject and moreover, it seems to be more widely used than I thought.
Respondent Driven Sampling (RDS) seems to be the most modern way of reaching hidden populations. In a RDS an initial sample is selected and those sampled subjects receive incentive to bring their peers who also belongs to the given population hidden. They get incentives if they answer the survey and if they successfully bring others subjects. RDS would be different from the Snowball Sample because the later ask subjects to name their peers, not to bring them over to the research site. This is an interesting paper to learn more about it.
Other sampling methods include Targeted Sampling where the research tries to make a preliminary list of eligible subjects and sample from there. Of course this is usually not very helpful because of costs and again the difficulty to reach some rare population. Key Informant Sampling is a sample where you would select, for example, people that work with the target population. They would give you information about the population, that is, you would not really sample subjects from the population, but instead would make your inferences through secondary sources of information. Time Space Sampling (TTS) is method where you list places and within those places, times when the target population can be reach. For example, a list of public eating places could be used to find homeless people and you know what time they can be reach. It is possible to have valid inferences for the population that goes to these places by sampling places and times interval in this list. You can see more about TTS sampling and find other references in this paper.
Now to a point about the paper I first mentioned, how good is RDS Sampling? Unfortunately the paper does not brings good news. According to the simulations they did, the variability of the RDS sample is quite high, with median design effect around 10. That means a RDS sample of size n would be as efficient (if we think about Margin of Error) as a Simple Random Sample of size n/10. That makes me start questioning the research, although the authors make good and valid points defending the assumptions they need to make so that their simulations becomes comparable to a real RDS. I don't know, I cannot say anything, but I wonder if out there a survey exist that has used RDS sample for several consecutive waves. I think this kind of survey would give us some ideas of the variability involved on replications of the survey. Maybe we could look at some traits that are not expected to change from wave to wave and make an assessment of its variability.
An interesting property of the RDS is that it tends to lose it bias with time. For example, it was noticed that if a black person is asked for referrals, the referrals tend to be more black the actual proportion of black people in the population. This seems to me a natural thing in networks, I mean, people tend to have peers that are similar to themselves. This will happen with some (or maybe most) of the demographics characteristics. But it looks like the evident bias present in the first wave of referrals seemingly disappear around the sixth wave. That seems to me to be a good thing and if the initial sample cannot be random maybe we should consider disregarding waves 1 to 5 or so.
Anyway, I think as of today researches still face huge technical challenges when the target population is rare. RDS and other methods of reaching these populations have been developed which helps a lot, but this remains an unresolved issue for statistician, one very important in sampling methodology.
Monday, 6 September 2010
Stepwise Regression
Never let the computer decide how your model should be. This is something I always try to stress in my daily work, meaning that we should include in our statistical models the knowledge that we have about the field we are working. The simplest example where we leave all decisions to the computer (or to the statistical program if you prefer) is when we run a stepwise regression.
Back in my school time it was just one of the ways we had to do variable selection in a regression model, when we had many variables. I did not consult the literature but my feeling is that by then people just were not aware of the problems of stepwise regression. Nowadays if you try to defend Stepwise Regression in a table with statisticians they will shoot you down.
It is not difficult to find papers discussion the problems of Stepwise. We have two examples here and here. I think one of the problems with Stepwise selection is the one I said above, it take out of the hands of the researcher the responsibility of thinking - the computer decides what should be in the model, what should not, using criteria not aways understood by those who runs the model. Another problems is the overfitting or capitalization on chance. Stepwise is often used when there are many variables and these are precisely the cases where you will easily have some variables in just by chance.
I ran a quick simulation on this. I generated a random dependent variables and 100 random independent variables and went on to run a stepwise regression using the random variables to explain the dependent variable. Of course we should not find any association here, all the variables are independent random variables. The histogram below show the R-square of the resulting model. If the sample size is 300 the R-Square will explain between 10% and 35% of the variability in Y. If the sample size is larger, say 1000 cases, then the effect of Stepwise is less misleading as the higher sample size protects against overfitting.
The overfitting is easily seem in Discriminant Analysis as well, which also has variable selection options.
There are at least two ways of avoiding this type of overfitting. One would be to include random variables in the data file and stop the stepwise whenever a random variable is selected. The other is to run the variable selection in a subset of the data file and validate the result using the rest. Unfortunately none of these procedures are easy to apply since current softwares does not allow you to stop the Stepwise when variable X enter the model and usually the sample size is too small to allow for a validation set.
Depending on the nature of the variable an interesting approach could be to run an exploratory Factor Analysis or Principal Component Analysis and include all the factors in the model.
Hopefully Stepwise Regression will be used with more caution if used at all. Below you have the SAS code I used to generate the simulations for these two histograms. I am not very good SAS programmer, I am sure someone can write this in a more elegant way... Sorry I did nto have time to insert comments...
%macro step;
%do step=1 %to &niter;
%put &step;
data randt;
array x[&nind] x1 - x&nind;
do i = 1 to &ncases;
y=rand('UNIFORM');
do j = 1 to &nind;
x[j] = rand('UNIFORM');
end;
output;
end;
run;
proc reg data = randt outest = est edf noprint;
model y = x1 - x&nind/selection = stepwise adjrsq;
run;
%if &step > 1 %then %do;
data comb;
set comb est;
run;
%end;
%else %do;
data comb;
set est;
run;
%end;
%end;
%mend step;
%let nind = 100;
%let ncases = 1000;
%let niter = 200;
%step;
Back in my school time it was just one of the ways we had to do variable selection in a regression model, when we had many variables. I did not consult the literature but my feeling is that by then people just were not aware of the problems of stepwise regression. Nowadays if you try to defend Stepwise Regression in a table with statisticians they will shoot you down.
It is not difficult to find papers discussion the problems of Stepwise. We have two examples here and here. I think one of the problems with Stepwise selection is the one I said above, it take out of the hands of the researcher the responsibility of thinking - the computer decides what should be in the model, what should not, using criteria not aways understood by those who runs the model. Another problems is the overfitting or capitalization on chance. Stepwise is often used when there are many variables and these are precisely the cases where you will easily have some variables in just by chance.
 |
| R-Square for 200 simulations where 100 random variables explain a dependent variable in a dataset with 1000 units. |
The overfitting is easily seem in Discriminant Analysis as well, which also has variable selection options.
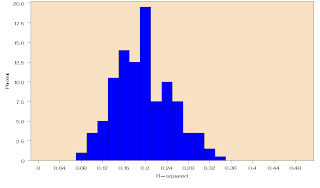 |
| R-Square for 200 simulations where 100 random variables explain a dependent variable in a data set of 300 units. |
Depending on the nature of the variable an interesting approach could be to run an exploratory Factor Analysis or Principal Component Analysis and include all the factors in the model.
Hopefully Stepwise Regression will be used with more caution if used at all. Below you have the SAS code I used to generate the simulations for these two histograms. I am not very good SAS programmer, I am sure someone can write this in a more elegant way... Sorry I did nto have time to insert comments...
%macro step;
%do step=1 %to &niter;
%put &step;
data randt;
array x[&nind] x1 - x&nind;
do i = 1 to &ncases;
y=rand('UNIFORM');
do j = 1 to &nind;
x[j] = rand('UNIFORM');
end;
output;
end;
run;
proc reg data = randt outest = est edf noprint;
model y = x1 - x&nind/selection = stepwise adjrsq;
run;
%if &step > 1 %then %do;
data comb;
set comb est;
run;
%end;
%else %do;
data comb;
set est;
run;
%end;
%end;
%mend step;
%let nind = 100;
%let ncases = 1000;
%let niter = 200;
%step;
proc univariate data=Work.Comb noprint;
var _RSQ_;
histogram / caxes=BLACK cframe=CXF7E1C2 waxis= 1 cbarline=BLACK cfill=BLUE pfill=SOLID vscale=percent hminor=0 vminor=0 name='HIST' midpoints = 0 to 0.5 by 0.01;
run;
Saturday, 4 September 2010
The "Little Jiffy" rule and Factor Analysis
Factor Analysis is a statistical technique we use all the time in Marketing Research. It is often the case that we want to uncover the dimensions in the consumer's mind that can help to explain variables of interest like Overall Satisfaction and Loyalty. Questionnaire are often cluttered with a whole bunch of attributes that makes the understanding of the analysis difficult and tiresome. To make matters worse it is not uncommon to see people wanting to run Regression Analysis with 20 or 30 attributes highly correlated. I don't want to talk about Regression here, but to me the only way out in these cases is to run a Factor Analysis and work with factors instead.
Back in my university years I learnt that Factor Analysis had to be rotated with Varimax Rotation, especially if you wanted to use the factor as independent variables in a Regression Analysis because this way the factors would have the optimum property of being orthogonal and their effects could be estimated purely in a Regression Analysis. Using the Varimax Rotation along with Principal Component Analysis and retaining as many factor as there are eigenvalues higher than 1 in the correlation matrix is the so called "Little Jiffy" approach for factor analysis. And it is widespread, you not only learn it in the school, you will see people using it all the time and you will find lots of papers following the approach. I remember this one from a research I did while doing some analyses for a paper.
In the workplace I soon noticed that you pay a price for having beautifully orthogonal factors to use in your regression: they are not always easy to be interpreted and even when the factors make sense they are not so sharply defined as one would like. It also makes more sense not to constrain factors to be independent because we have no evidence that if these factors exist in real world they are orthogonal. So I abandoned the orthogonal rotation.
The number of factors to retain is something more subtle. I think the eigenvalue higher than 1 rule usually gives a good starting point for the Exploratory Factor Analysis, but I like to look at several solutions and choose the one easier to interpret as the factor has to be understood as it will be target for actions on the client side.
Finally I want to link to this paper, which is an interesting source for those who works with Factor Analysis. There is something in the example (with measures of boxes...) that I don't like, maybe the non linear dependence of some measure on others would tell us that we should not expect Factor Analysis to perform well. It would be better to simulate data clearly following a certain factor model structure and explore it instead.
Do not let the computer decide what to do with the data, by using the Little Jiffy rule of thumb, instead take a more proactive approach and bring your knowledge in, don't be afraid to think your problem and what makes more sense in your specific situation.
Back in my university years I learnt that Factor Analysis had to be rotated with Varimax Rotation, especially if you wanted to use the factor as independent variables in a Regression Analysis because this way the factors would have the optimum property of being orthogonal and their effects could be estimated purely in a Regression Analysis. Using the Varimax Rotation along with Principal Component Analysis and retaining as many factor as there are eigenvalues higher than 1 in the correlation matrix is the so called "Little Jiffy" approach for factor analysis. And it is widespread, you not only learn it in the school, you will see people using it all the time and you will find lots of papers following the approach. I remember this one from a research I did while doing some analyses for a paper.
In the workplace I soon noticed that you pay a price for having beautifully orthogonal factors to use in your regression: they are not always easy to be interpreted and even when the factors make sense they are not so sharply defined as one would like. It also makes more sense not to constrain factors to be independent because we have no evidence that if these factors exist in real world they are orthogonal. So I abandoned the orthogonal rotation.
The number of factors to retain is something more subtle. I think the eigenvalue higher than 1 rule usually gives a good starting point for the Exploratory Factor Analysis, but I like to look at several solutions and choose the one easier to interpret as the factor has to be understood as it will be target for actions on the client side.
Finally I want to link to this paper, which is an interesting source for those who works with Factor Analysis. There is something in the example (with measures of boxes...) that I don't like, maybe the non linear dependence of some measure on others would tell us that we should not expect Factor Analysis to perform well. It would be better to simulate data clearly following a certain factor model structure and explore it instead.
Do not let the computer decide what to do with the data, by using the Little Jiffy rule of thumb, instead take a more proactive approach and bring your knowledge in, don't be afraid to think your problem and what makes more sense in your specific situation.
Saturday, 14 August 2010
Interesting figures
When analyzing cross-sectional surveys I am well familiar with the "bias" of significant results caused by the excess of search for them. Negatives and neutral results are ignored and the positive results are always reported. With thousands of possible results in a simple survey it is obvious that the Type I error will happen quite often.
When testing a statistical hypotheses the theory tells us that we should first establish the hypothesis, then collect the data and finally test the hypothesis using the data. If we look at the data prior to establishing the hypothesis the probabilities associated with statistical test are no longer valid and significant results might easily be only random fluctuations.
Ok, related to that, I read today in this book (See page 101) about a comparison between randomized studies and not controlled ones. I could not access any of the papers on table 3.4.1, but the results shown are expected anyway. If studies are not controlled many more positive results will be found, compared with randomized studies where the statistical theory of experimental design is followed as close as possible. If statistical hypothesis and statistical procedures needed to test them are not decided upon up front as is usually the case of randomized trials, lots of room is created for human interference either by changing hypotheses to others that are confirmed by the results or by making use of confounded results in favor of the seek results.
I think this table shows the importance of planned experiment on testing hypothesis and how careful we should be when analyzing non experimental data. At the same time we need to recognize that experimental studies are not always possible because of costs, time or even because they are not really possible. This makes the analysis of cross-sectional data necessary and very valuable. In causal analysis, though, we need to be aware of the drawbacks of analyzing this type of data.
When testing a statistical hypotheses the theory tells us that we should first establish the hypothesis, then collect the data and finally test the hypothesis using the data. If we look at the data prior to establishing the hypothesis the probabilities associated with statistical test are no longer valid and significant results might easily be only random fluctuations.
Ok, related to that, I read today in this book (See page 101) about a comparison between randomized studies and not controlled ones. I could not access any of the papers on table 3.4.1, but the results shown are expected anyway. If studies are not controlled many more positive results will be found, compared with randomized studies where the statistical theory of experimental design is followed as close as possible. If statistical hypothesis and statistical procedures needed to test them are not decided upon up front as is usually the case of randomized trials, lots of room is created for human interference either by changing hypotheses to others that are confirmed by the results or by making use of confounded results in favor of the seek results.
I think this table shows the importance of planned experiment on testing hypothesis and how careful we should be when analyzing non experimental data. At the same time we need to recognize that experimental studies are not always possible because of costs, time or even because they are not really possible. This makes the analysis of cross-sectional data necessary and very valuable. In causal analysis, though, we need to be aware of the drawbacks of analyzing this type of data.
Saturday, 7 August 2010
New book
I started reading another book about Clinical Trials. At least I heard better comments about this one. Design and Analysis of Clinical Trials is a book written in a more professional language and it seems to explain Clinical Trials in depth, covering much broader areas than statistics.
I read the first chapter so far and it talks about clinical trials regulatory rules of FDA in US. It describes the structure of FDA and the steps it takes to have a new drug approved in the marketing. It also talks about length of the process and it phases. I was surprised that the average time spent on drug development before it is launched in the market is about 12 years. It is a lot of time and a lot of money. This is quite interesting for anyone who wants to understand this process of getting a new drug in the marketing and if the content is not enough there are references.
The second chapter is about basic statistical concept and I was less than happy with the way the authors explained variance, bias, validity and reliability. I have some disagreements with the text, like using variability interchangeably with variance. To me the text does not explain these very important concepts in a satisfactory way. One might think that the book is directed to non math people so it should not go deep into these things, but I disagree; I think it might open a door for bad statistics practice, as if we did not have enough. The other example is when they talk about the bias caused by the fact that the trial was planned to take place in three cities but it turned out that one of them did not have enough volunteer, so they increased the sample in the other two cities. They say this might have caused a bias. But they do not define clearly the target population, the target variables to be measured, the reasons of the bias when excluding one city. To me, if we are talking about clinical trials to test a new drug, we have to define the target population for this drug to begin with. It is the set of people that have the disease X, say. Of course these folks are not only in three cities, so how do you explain that sampling only three cities does not bring a bias? It is possible, if they define the cities as the only important target for the new drug, but I don't think this is likely to be reasonable. They could also lay down their argument as to why these three cities only would represent fairly the US for this given health condition. Anyway, they talked about biases but very important things were left aside and this is a very important concept when sampling under restrictions (I see clinical trials as something that can almost never have a good probabilistic sample, so concepts like biases are crucial).
I liked the first chapter and so far what is in the second chapter is not what I was expecting to learn from the book, so I will keep reading it. The topics ahead in the book are of great interest to me, like type of designs, randomization, specific type of trials for cancer, and so on. I will try to comment as I read the chapters.
I read the first chapter so far and it talks about clinical trials regulatory rules of FDA in US. It describes the structure of FDA and the steps it takes to have a new drug approved in the marketing. It also talks about length of the process and it phases. I was surprised that the average time spent on drug development before it is launched in the market is about 12 years. It is a lot of time and a lot of money. This is quite interesting for anyone who wants to understand this process of getting a new drug in the marketing and if the content is not enough there are references.
The second chapter is about basic statistical concept and I was less than happy with the way the authors explained variance, bias, validity and reliability. I have some disagreements with the text, like using variability interchangeably with variance. To me the text does not explain these very important concepts in a satisfactory way. One might think that the book is directed to non math people so it should not go deep into these things, but I disagree; I think it might open a door for bad statistics practice, as if we did not have enough. The other example is when they talk about the bias caused by the fact that the trial was planned to take place in three cities but it turned out that one of them did not have enough volunteer, so they increased the sample in the other two cities. They say this might have caused a bias. But they do not define clearly the target population, the target variables to be measured, the reasons of the bias when excluding one city. To me, if we are talking about clinical trials to test a new drug, we have to define the target population for this drug to begin with. It is the set of people that have the disease X, say. Of course these folks are not only in three cities, so how do you explain that sampling only three cities does not bring a bias? It is possible, if they define the cities as the only important target for the new drug, but I don't think this is likely to be reasonable. They could also lay down their argument as to why these three cities only would represent fairly the US for this given health condition. Anyway, they talked about biases but very important things were left aside and this is a very important concept when sampling under restrictions (I see clinical trials as something that can almost never have a good probabilistic sample, so concepts like biases are crucial).
I liked the first chapter and so far what is in the second chapter is not what I was expecting to learn from the book, so I will keep reading it. The topics ahead in the book are of great interest to me, like type of designs, randomization, specific type of trials for cancer, and so on. I will try to comment as I read the chapters.
Sunday, 25 July 2010
Survey Subject and Non Response Error
Statisticians usually have a skeptical opinion about web surveys, the most common type of survey nowadays in North America. That is because there is virtually no sampling theory that can accommodate the "sampling design" of a Web Survey without making strong assumptions well known not to hold in many situations. But in a capitalist world the cost drives everything and drives also the way we draw our samples. If you think about the huge economy a Web survey can proportionate you will agree that the "flawed" sample can be justified - it is just a trade off between cost and precision. Hopefully those who are buying the survey are aware of that, and here is where the problem is, as I see it.
The trade off can be very advantageous indeed because it has been shown that in some cases a Web Survey can approximate reasonably the results a probabilistic sample. Our experience is crucial on the understanding of when we should be concerned with web survey results and how to make them more in line with probability samples. This paper, for example, shows that results from attitudinal questions from a web panel sample are quite close to a probability survey. But no doubt we can not hope to be able to use the mathematical theory that allows us to pinpoint the precision of the study.
Challenges are never enough though. In an effort to reduce the burden of the survey to the respondent, researchers are disclosing the subject of the survey before its beginning so that the respondent can decide whether of not to participate. The expected time of the survey is another information often released before the survey starts. Now the respondent that does not like the survey subject or does not feel like responding about it can just send the survey invitation to the trash can. But, what the possible consequences of this are?
Non response biases can be huge. Suppose, for example, a survey about groceries. Pretty much everybody buys grocery and would be eligible for participating in such a survey but possibly not everybody like to do it. The probability that someone that likes to shop for groceries has to participate in such a survey, if the subject is disclosed, we can argue, is much higher than the probability of somebody that thinks it is just a chore to participate. If the incidence of "grocery shopping lovers" in the population is, say, 20%, it will likely be much higher in the sample, without any possibility of being corrected through weighting. Shopping habits and attitudes will likely be associated to some extent to how much people like to shop and this will likely cause a bias in the survey.
Disclosing the subject in a web survey is almost certainly the same as biasing the results in a way that can not be corrected or quantified. Yet again the technical aspect of sampling is put aside without fully understanding its consequences. Yet again the accuracy of estimates is second to the business priorities and yet again we face the challenge of making useful the results of surveys that cross unknown boundaries...
The trade off can be very advantageous indeed because it has been shown that in some cases a Web Survey can approximate reasonably the results a probabilistic sample. Our experience is crucial on the understanding of when we should be concerned with web survey results and how to make them more in line with probability samples. This paper, for example, shows that results from attitudinal questions from a web panel sample are quite close to a probability survey. But no doubt we can not hope to be able to use the mathematical theory that allows us to pinpoint the precision of the study.
Challenges are never enough though. In an effort to reduce the burden of the survey to the respondent, researchers are disclosing the subject of the survey before its beginning so that the respondent can decide whether of not to participate. The expected time of the survey is another information often released before the survey starts. Now the respondent that does not like the survey subject or does not feel like responding about it can just send the survey invitation to the trash can. But, what the possible consequences of this are?
Non response biases can be huge. Suppose, for example, a survey about groceries. Pretty much everybody buys grocery and would be eligible for participating in such a survey but possibly not everybody like to do it. The probability that someone that likes to shop for groceries has to participate in such a survey, if the subject is disclosed, we can argue, is much higher than the probability of somebody that thinks it is just a chore to participate. If the incidence of "grocery shopping lovers" in the population is, say, 20%, it will likely be much higher in the sample, without any possibility of being corrected through weighting. Shopping habits and attitudes will likely be associated to some extent to how much people like to shop and this will likely cause a bias in the survey.
Disclosing the subject in a web survey is almost certainly the same as biasing the results in a way that can not be corrected or quantified. Yet again the technical aspect of sampling is put aside without fully understanding its consequences. Yet again the accuracy of estimates is second to the business priorities and yet again we face the challenge of making useful the results of surveys that cross unknown boundaries...
Monday, 19 July 2010
Census - The polemic of the long form
Next year is the year of the Census in Canada. The Canadian Census is conducted every 5 years and used to be composed of a long questionnaire and a short questionnaire. Both were mailed to the respondents who had to respond, since it was mandatory. While the short form were sent to every household, the long form were sent to only one fifth of the households, so it was a Survey rather than a Census.
Now they decided that the long questionnaire will be voluntary and will be sent to one third of the households. The main argument is that there are people who considers the long form particularly intrusive, with too personal questions. It had 40 pages in 2006. But this argument seemed not to be enough and the subject became a huge polemic. Concerns about results accuracy and continuity of historical trend are among the main points among those who are against a voluntary long form.
A good statistical point against the voluntary survey is that it is not only supposed to be a very accurate picture of Canadians but it is also a very important base for many other surveys, official or not. Until the results of the new Census in 2016 come along, Statistics Canada itself will be relying on the long 2011 form results as a baseline for designing and weighting their other surveys.
I have to say that I am not sure what precisely "voluntary" means in this case, in particular, what will be the effort done to get people to answer to the long form. What would the expected response rate be? It seems that Statistics Canada can get pretty good response rates even with voluntary surveys, and if that is so maybe there is no reason for concerns. We have to remember, though, that they are increasing from 1/5 to 1/3 the number of questionnaires sent, and that seems to mean they are expecting a sizable non response rate. Even with all the weighting development we have nowadays, I would think they should do a test or try to estimate somehow the non response rate, and the decision as to whether or not to go mandatory would depend on that. I think this particular Survey cannot afford to be questionable on its methodology.
Back on the time I was at the graduating school, I had a professor that said a Survey would be as accurate as a Census and cost much less. That was also back in Brazil where Censuses are not mandatory. It seems to me that it could be a Survey as long as it was mandatory or as long as it had a very high response rate. One of the arguments against the Census is that it is actually not precise at all, with lots of people not answering to it, or not telling the truth. I think the biases from this kind of thing would be really minor, much lower than the possible biases in a survey with low response rate. So I think things are not as simple as replacing censuses by surveys, there are some serious concern involved. Not to say that making people answer a survey could in fact increase non response error since we could think that people that don't want to respond could "lie" if forced to respond.
Back to the Canadian polemic, it seems possible that there are some political reasons for the changes (rather than only technical), which is of concern. Anyway, let's hope scientific concern drives the choice of the method. I am sure there are very good statistician behind this and I hope they can be heard.
Now they decided that the long questionnaire will be voluntary and will be sent to one third of the households. The main argument is that there are people who considers the long form particularly intrusive, with too personal questions. It had 40 pages in 2006. But this argument seemed not to be enough and the subject became a huge polemic. Concerns about results accuracy and continuity of historical trend are among the main points among those who are against a voluntary long form.
A good statistical point against the voluntary survey is that it is not only supposed to be a very accurate picture of Canadians but it is also a very important base for many other surveys, official or not. Until the results of the new Census in 2016 come along, Statistics Canada itself will be relying on the long 2011 form results as a baseline for designing and weighting their other surveys.
I have to say that I am not sure what precisely "voluntary" means in this case, in particular, what will be the effort done to get people to answer to the long form. What would the expected response rate be? It seems that Statistics Canada can get pretty good response rates even with voluntary surveys, and if that is so maybe there is no reason for concerns. We have to remember, though, that they are increasing from 1/5 to 1/3 the number of questionnaires sent, and that seems to mean they are expecting a sizable non response rate. Even with all the weighting development we have nowadays, I would think they should do a test or try to estimate somehow the non response rate, and the decision as to whether or not to go mandatory would depend on that. I think this particular Survey cannot afford to be questionable on its methodology.
Back on the time I was at the graduating school, I had a professor that said a Survey would be as accurate as a Census and cost much less. That was also back in Brazil where Censuses are not mandatory. It seems to me that it could be a Survey as long as it was mandatory or as long as it had a very high response rate. One of the arguments against the Census is that it is actually not precise at all, with lots of people not answering to it, or not telling the truth. I think the biases from this kind of thing would be really minor, much lower than the possible biases in a survey with low response rate. So I think things are not as simple as replacing censuses by surveys, there are some serious concern involved. Not to say that making people answer a survey could in fact increase non response error since we could think that people that don't want to respond could "lie" if forced to respond.
Back to the Canadian polemic, it seems possible that there are some political reasons for the changes (rather than only technical), which is of concern. Anyway, let's hope scientific concern drives the choice of the method. I am sure there are very good statistician behind this and I hope they can be heard.
Friday, 16 July 2010
I give up
I could not keep reading the book Statistics Applied to Clinical Trial. I had commented here that I hadn't liked the book since its first chapter, but from chapter 8 to chapter 13 the book becomes a joke. I could not read more.
Even if the Statistical Concepts were explained correctly, the book is written in a very confusing and repetitive way. Chapters 8 and 9 talk about the same thing, which Chapter 9 repeating lots of things in Chapter 8. The same thing happens again on Chapters 10, 11 and 12.
The authors ignores important concepts in Statistics. For example when they say " The p-value tells us the chance of making a type I error of finding a difference where there is none.". The p-value is in fact the probability of finding a difference as big as the one found, or bigger, given H0. P-value = P(Data/H0 True) not P(H0 True/Data). They talk a little bit about the non use of standards like 5% for significance test, but they go on and on always using the rule of 5%. They say that p-values too high is a proof that something is wrong with the study but in Hypothesis test we need to define our hypotheses and how to test them and calculate power and everything a priori. If you do not account for rejection of high p-values before the survey, it is not valid to look at the p-value after the fact and say "Well, I was expecting the p-value to be lower than 5% but it turned out to be 99%, so this is too high and I will Reject H0 because the chance of a p-value higher than 98% given H0 is too small". Perhaps a high p-value could be used as part of descriptive analysis, a red flag saying that maybe we should see if there is no obvious reason to get results so in line with H0.
They say that Correlation and Regression do not show causality but simple association (they do not use the word association, but correlation). They go on saying the Hypothesis tests with Clinical Trials is the real thing to detect causality. But, what is the difference between the ANOVA in a Clinical Trial and Regression? This is simply a huge confusion between observational data and experimental data, and they think Regression is used only with Observational Data in spite of not knowing Regression and ANOVA is the same thing. Ok, maybe they don't think Regression is only for observational data since they go on using Regression in an Cross-over trial. The dependent variable is the first measure and the independent is the second measure, showing that they do not have a sense of what is dependent variable and what is independent variable. If you want the Regression to make sense here, the independent variable has to be the treatments and this has to be a Hierarchical Regression with Within subject effects. That is, the Regression they use for their examples are meaningless. Not to mention the fact that they do not interpret the betas.
Finally I want to say that the book is confusing. The reader do not learn how to do a statistical test or a regression because the formulas appear from nowhere. I had trouble to understand how they use the formulas, imagine someone that is not a statistician.
Frustrated with the dissemination of bad use of statistics and wrong concepts, I wrote my negative review of the book on Amazon website. Hopefully others will choose better than me.
Even if the Statistical Concepts were explained correctly, the book is written in a very confusing and repetitive way. Chapters 8 and 9 talk about the same thing, which Chapter 9 repeating lots of things in Chapter 8. The same thing happens again on Chapters 10, 11 and 12.
The authors ignores important concepts in Statistics. For example when they say " The p-value tells us the chance of making a type I error of finding a difference where there is none.". The p-value is in fact the probability of finding a difference as big as the one found, or bigger, given H0. P-value = P(Data/H0 True) not P(H0 True/Data). They talk a little bit about the non use of standards like 5% for significance test, but they go on and on always using the rule of 5%. They say that p-values too high is a proof that something is wrong with the study but in Hypothesis test we need to define our hypotheses and how to test them and calculate power and everything a priori. If you do not account for rejection of high p-values before the survey, it is not valid to look at the p-value after the fact and say "Well, I was expecting the p-value to be lower than 5% but it turned out to be 99%, so this is too high and I will Reject H0 because the chance of a p-value higher than 98% given H0 is too small". Perhaps a high p-value could be used as part of descriptive analysis, a red flag saying that maybe we should see if there is no obvious reason to get results so in line with H0.
They say that Correlation and Regression do not show causality but simple association (they do not use the word association, but correlation). They go on saying the Hypothesis tests with Clinical Trials is the real thing to detect causality. But, what is the difference between the ANOVA in a Clinical Trial and Regression? This is simply a huge confusion between observational data and experimental data, and they think Regression is used only with Observational Data in spite of not knowing Regression and ANOVA is the same thing. Ok, maybe they don't think Regression is only for observational data since they go on using Regression in an Cross-over trial. The dependent variable is the first measure and the independent is the second measure, showing that they do not have a sense of what is dependent variable and what is independent variable. If you want the Regression to make sense here, the independent variable has to be the treatments and this has to be a Hierarchical Regression with Within subject effects. That is, the Regression they use for their examples are meaningless. Not to mention the fact that they do not interpret the betas.
Finally I want to say that the book is confusing. The reader do not learn how to do a statistical test or a regression because the formulas appear from nowhere. I had trouble to understand how they use the formulas, imagine someone that is not a statistician.
Frustrated with the dissemination of bad use of statistics and wrong concepts, I wrote my negative review of the book on Amazon website. Hopefully others will choose better than me.
Saturday, 10 July 2010
Interim Analysis
In the world of Clinical Trials there is a type of Statistical Analysis they call Interim Analysis. It is concerned with analyzing the results of the trial before its end in order to assure the protocols of the study are being followed and to see whether the results at a given point in time are already strongly favoring or opposing the study hypothesis to the point that the experiment could stop and save money, perhaps saving lives too. For example, if we have strong evidence that treatment A is better than treatment B, then there is no point on continuing the trial, which gives half of participants the less efficient treatment B.
An Interim Analysis differs a little from usual statistical analysis of clinical trials, even though it is a type of statistical analysis. Interim Analysis is not as complete as the statistical analyses performed at the end of the trial and it usually does not aim to understand many outcome variables. One of the reasons is that it is not supposed to be too expensive and another is that it is not supposed to influence the trial. Interim Analysis has to be done preserving the blindness of the trial, therefore in an almost confidential way. Trials with a great amount of analysis before its completion may be questioned as to the extent the external procedures of analyzing data did not influence the trial itself.
As such an Interim Analysis often focus on some main outcome variables at limited points in time. It wants to avoid multiple comparison problems and its protocol must be very well defined in advance. Strict rules of analysis and stopping rules (i.e. if this comparison is found significant the trial must stop) are well defined and followed.
One of the most used types of Interim Analysis is the Group Sequential Analysis. It is defined a priori how many analyses will be performed during the trial and the sample size per treatment at the point when the analyses is done. Based on this stopping rules can be defined in terms of level of significance attained at each and every analysis.
Another type is called Continuous Sequential Statistical Techniques, which, as I see does not go without some criticism. Here, at the arrival of each new results the entire set of data is reanalyzed and differences reaccessed. Cut off for the lower and upper bound of difference are established that when reached causes the trial to stop because a conclusion is already clear - either the treatment is significantly better or worse than the other. This seems to be a good book on this subject.
An Interim Analysis differs a little from usual statistical analysis of clinical trials, even though it is a type of statistical analysis. Interim Analysis is not as complete as the statistical analyses performed at the end of the trial and it usually does not aim to understand many outcome variables. One of the reasons is that it is not supposed to be too expensive and another is that it is not supposed to influence the trial. Interim Analysis has to be done preserving the blindness of the trial, therefore in an almost confidential way. Trials with a great amount of analysis before its completion may be questioned as to the extent the external procedures of analyzing data did not influence the trial itself.
As such an Interim Analysis often focus on some main outcome variables at limited points in time. It wants to avoid multiple comparison problems and its protocol must be very well defined in advance. Strict rules of analysis and stopping rules (i.e. if this comparison is found significant the trial must stop) are well defined and followed.
One of the most used types of Interim Analysis is the Group Sequential Analysis. It is defined a priori how many analyses will be performed during the trial and the sample size per treatment at the point when the analyses is done. Based on this stopping rules can be defined in terms of level of significance attained at each and every analysis.
Another type is called Continuous Sequential Statistical Techniques, which, as I see does not go without some criticism. Here, at the arrival of each new results the entire set of data is reanalyzed and differences reaccessed. Cut off for the lower and upper bound of difference are established that when reached causes the trial to stop because a conclusion is already clear - either the treatment is significantly better or worse than the other. This seems to be a good book on this subject.
Sunday, 4 July 2010
Equivalence Tests
Reading the Book Statistics Applied to Clinical Trials I learnt about Equivalence tests. This is very interesting indeed. Situations exists where you want to test whether a treatment has the same effect compared to a placebo or compared to an existing treatment. This can be readily extended to situation I face on my daly work with Marketing Research.
For example, suppose the client wishes to change the methodology of their survey from telephone to Online interviews. This will make things much cheaper, but will it make results from the new methodology incomparable with results from the old methodology? To test that we can simply conduct surveys with both methodology at the same time. But then, how do you compare them as to say their results "are the same"?
I soon realized that the usual statistical test of hypothesis is not suitable for this kind of situation. So I quickly thought about something. My approach was to do the usual statistical test, but lowering the confidence level to, say, 70%. I want my test to have more power, so that when I stay with the null hypothesis I am more confident it is true. But to tell the truth I have never even used this because of tremendous difficult to explain people why the usual test is not correct and why this would be a better approach. The problem may be more that 70% is something that seems not as good as 95%, at least from the eyes of non statisticians. Then I came up with a second approach which I used a few times. Ok, we will do the usual stat test, but we will do it several times. We compare the surveys for 3 or 5 months and this will tell us whether there is a methodology effect, even if it is not statistically significant. The approach seemed to work, I could see in one case that the new method produced slight lower averages that were not statistically significant though. Now we have a better idea of how much interview methodology affects survey results and we can even make the decision without relying on statistical tests.
Comparison of interview methodology is just one thing that requires equivalence testing. Many others exists, specially in product testing, when the company wants to launch a new product that is cheaper to produce and we need to test whether the perception of the consumer will be the same.
The approach for Clinical Trials, as showed in this book, is different and easier in a way. You first define what a significant difference would be from practical (not statistical) point of view. One might say, for example, that if differences are lower than 3% they can be considered as equal. Now we can construct a confidence interval for the difference of the means and if this interval is within the range [-3%;3%] we can consider things equivalent. I have to say, though, that this tolerance range is not easy to define in some cases, to the point that I am not sure this could be applied on my type of problems. But I might try.
I searched the internet for equivalence testing and found that there are other ways of doing the test. The book just explained the simplest way of doing it (as I would expect - read the critics I made to the book) and perhaps the oldest way. But the good thing is that it showed me the issue and I can look for it elsewhere...
For example, suppose the client wishes to change the methodology of their survey from telephone to Online interviews. This will make things much cheaper, but will it make results from the new methodology incomparable with results from the old methodology? To test that we can simply conduct surveys with both methodology at the same time. But then, how do you compare them as to say their results "are the same"?
I soon realized that the usual statistical test of hypothesis is not suitable for this kind of situation. So I quickly thought about something. My approach was to do the usual statistical test, but lowering the confidence level to, say, 70%. I want my test to have more power, so that when I stay with the null hypothesis I am more confident it is true. But to tell the truth I have never even used this because of tremendous difficult to explain people why the usual test is not correct and why this would be a better approach. The problem may be more that 70% is something that seems not as good as 95%, at least from the eyes of non statisticians. Then I came up with a second approach which I used a few times. Ok, we will do the usual stat test, but we will do it several times. We compare the surveys for 3 or 5 months and this will tell us whether there is a methodology effect, even if it is not statistically significant. The approach seemed to work, I could see in one case that the new method produced slight lower averages that were not statistically significant though. Now we have a better idea of how much interview methodology affects survey results and we can even make the decision without relying on statistical tests.
Comparison of interview methodology is just one thing that requires equivalence testing. Many others exists, specially in product testing, when the company wants to launch a new product that is cheaper to produce and we need to test whether the perception of the consumer will be the same.
The approach for Clinical Trials, as showed in this book, is different and easier in a way. You first define what a significant difference would be from practical (not statistical) point of view. One might say, for example, that if differences are lower than 3% they can be considered as equal. Now we can construct a confidence interval for the difference of the means and if this interval is within the range [-3%;3%] we can consider things equivalent. I have to say, though, that this tolerance range is not easy to define in some cases, to the point that I am not sure this could be applied on my type of problems. But I might try.
I searched the internet for equivalence testing and found that there are other ways of doing the test. The book just explained the simplest way of doing it (as I would expect - read the critics I made to the book) and perhaps the oldest way. But the good thing is that it showed me the issue and I can look for it elsewhere...
Saturday, 3 July 2010
How to do it
Considering the post below, this is how variance estimation under Simple Random Sample design can be performed (as per post below). Here we use Taylor Linearization but others methods are also available.
In R, load package "Survey"
library(survey)
attach(mydata)
mydesign<-svydesign(id=idnumber,weights = wgtem,data=mydata)
svymean(varx,design = mydesign) #mean and standard error for varx.
svyby(~varx,~agex,mydesign,svymean) #now by age.
Using Stata:
svyset idnumber [pweight=wgtem], vce(linearized)
svy, vce(linearized): mean varx, over(agex)
Agex are age ranges, varx is the variable for which we want to calculate the mean. wgtem is the weighting variable. I have found interesting looking at the Design Effect as a measure of weight efficiency. If Design Effect is too high than maybe we should consider collapsing levels of variables to get less extreme weighting factors. If you want to calculate Design Effect make sure your weights add up to the total target population.
In R, load package "Survey"
library(survey)
attach(mydata)
mydesign<-svydesign(id=idnumber,weights = wgtem,data=mydata)
svymean(varx,design = mydesign) #mean and standard error for varx.
svyby(~varx,~agex,mydesign,svymean) #now by age.
Using Stata:
svyset idnumber [pweight=wgtem], vce(linearized)
svy, vce(linearized): mean varx, over(agex)
Agex are age ranges, varx is the variable for which we want to calculate the mean. wgtem is the weighting variable. I have found interesting looking at the Design Effect as a measure of weight efficiency. If Design Effect is too high than maybe we should consider collapsing levels of variables to get less extreme weighting factors. If you want to calculate Design Effect make sure your weights add up to the total target population.
Weights in Non Probabilistic Surveys
The fact that we really do not have a standard procedure to deal with precision of estimates in Non Probabilistic Samples has bothered me for some time. In the business world there is not a single survey that is true probabilistic and few of them are close enough that we feel comfortable making the assumption of probabilistic samples.
Samples are often weighted to some standard demographic variables, like age, gender and region. And this brings another layer of difficulty since now precision measures are not only calculated in a Non probabilistic sample, but it is also calculated without accounting for the weights.
Recognizing that Probabilistic Samples are not the reality of our world, we need to be pragmatic and use our knowledge of Sampling Theory to get the most we can from whichever sample we manage to get. If we are comfortable enough to make the assumption that the sample is not strongly biased then I believe it makes sense to think about variability and margin of error, even if they have to be labeled at the bottom of the page with an asterisk that states our assumptions. But, assuming fair to calculate variability, how do we proceed on with the variance calculation in presence of weights?
I have not found much literature on this, likely because Non Probabilistic Samples are mostly ignored as being practice of people that does not know Sampling Theory (I might comment more on that in another future post). But I do know that the only weight applied to these surveys is the post stratification weights, were some demographics (and rarely other things) are corrected to mirror some official figures. When weights are based only on Age and Gender, for example, it makes sense to me to analyze the results as a Stratified Random Sample where Age and Gender are interlocked strata. Often, though, they are not weighted jointly, using a two way table, but through their marginal distribution. Still I think it might make sense to define each different weight factor as a different stratum when calculating variability.
More problems arise when we weight marginals of many variables. Defining different weights as different stratum is not doable anymore since we can have hundreds of strata. In this case I have done some tests using SPSS Complex Sample and Stata and declaring the sample as being Simple Random Sample, as if the weights were the simply the inverse of the probability of selection. Variance calculated in this way are for sure much more realistic that the ones SPSS or Stata calculates with what they call frequency weights. Defining post stratification weights as frequency weights in variance calculation is everything we need to get the wrong figures and fool ourselves.
Usually the Simple Random Sample specification will show how weighting data increases the variances. This is a big improvement over not weighting or considering weights as frequency, even though it might not be the best improvement one can have. To me now we are down to a more difficult question which is the question about the validity of the assumptions we need to make to be able to calculate variances and take them as good estimates of population parameters. But this can be the subject of another post...
Samples are often weighted to some standard demographic variables, like age, gender and region. And this brings another layer of difficulty since now precision measures are not only calculated in a Non probabilistic sample, but it is also calculated without accounting for the weights.
Recognizing that Probabilistic Samples are not the reality of our world, we need to be pragmatic and use our knowledge of Sampling Theory to get the most we can from whichever sample we manage to get. If we are comfortable enough to make the assumption that the sample is not strongly biased then I believe it makes sense to think about variability and margin of error, even if they have to be labeled at the bottom of the page with an asterisk that states our assumptions. But, assuming fair to calculate variability, how do we proceed on with the variance calculation in presence of weights?
I have not found much literature on this, likely because Non Probabilistic Samples are mostly ignored as being practice of people that does not know Sampling Theory (I might comment more on that in another future post). But I do know that the only weight applied to these surveys is the post stratification weights, were some demographics (and rarely other things) are corrected to mirror some official figures. When weights are based only on Age and Gender, for example, it makes sense to me to analyze the results as a Stratified Random Sample where Age and Gender are interlocked strata. Often, though, they are not weighted jointly, using a two way table, but through their marginal distribution. Still I think it might make sense to define each different weight factor as a different stratum when calculating variability.
More problems arise when we weight marginals of many variables. Defining different weights as different stratum is not doable anymore since we can have hundreds of strata. In this case I have done some tests using SPSS Complex Sample and Stata and declaring the sample as being Simple Random Sample, as if the weights were the simply the inverse of the probability of selection. Variance calculated in this way are for sure much more realistic that the ones SPSS or Stata calculates with what they call frequency weights. Defining post stratification weights as frequency weights in variance calculation is everything we need to get the wrong figures and fool ourselves.
Usually the Simple Random Sample specification will show how weighting data increases the variances. This is a big improvement over not weighting or considering weights as frequency, even though it might not be the best improvement one can have. To me now we are down to a more difficult question which is the question about the validity of the assumptions we need to make to be able to calculate variances and take them as good estimates of population parameters. But this can be the subject of another post...
Friday, 2 July 2010
Statistics and Clinical Trials
I am reading the book Statistics Applied to Clinical Trials due to my great interest in the subject. I chose this book because it is a new edition and the index seemed to reflect closely what I expected to learn. But the book has disappointed me to some extent even though I am still finding it useful. The technical aspect of statistics is sometimes neglected or at least its presentation does not follow a standard: sometimes we see technical stuff without much explanation, without rigor and sometimes when we wish to see the math, it is not there. Formulas are frequently showed in a messy and difficult to understand way. Even though the authors do a good job on explaining the correct interpretation of hypothesis tests, they are too tied to the 5% and 1% rule as if it were universal. Sometimes they interpret p-value in the wrong way.
All of that is bad in a way because we are not sure we can trust the part of the book where we have less fluency. It has been a easy read though (will be for anyone with some background in statistics) and I think despite of the poor quality I have been exposed to, it is worth the time.
I might comment more on specific chapters...
New blog, new ideas
I am starting this blog with a new goal and I hope to be commited to it. I want to leave here things that I learn on statistics and other fields of interest. I have this passion for reading books and navigating the internet and learning and I want to register it. While comments are always appreciated my goal is not to be a populat blogger but rather to have the opportunity to write down new things that make me grow everyday.
My other blog is more of a personal and informal one. There I write day to day experiences and thoughts. Here it will be more about knowledge, about statistics, about what I read.
Looping Infinito is also writen in Portuguese because it is above all a link to my roots, my friend and my language that is the most beautiful language. This space is different, it is more about specific knowledge, it is more serious, more technical if you will. I dont expect to go crazy on math theory (not sure I could anyway) but I do expect to comment on things that are restricted to few people's interest (if we consider the entire world population). So I thought I was better off writing it on English, this universal language that can reach out the world. I think these more technical subjects will make writing in English easier to me, given that I have my limitations.
If not many people ends up reading what I write, this space will still serve its objective - make me think, because it is necessary to think more when we need to summarize what we learnt. And this will make me learn more.
Subscribe to:
Comments (Atom)