Yesterday I was listening to a program on CBC Radio about a new treatment for Multiple Sclerosis. The program is indeed very interesting and exposes the widespread problem of non scientific news in the scientific world.
The new treatment for Multiple Sclerosis conducted by the Italian Doctor Zamboni has gained considerable space in the media and this is not the first time I hear about it. While there are some people saying that they got substantial improvement through the treatment, the public health system in Canada refuses to conduct the procedure under the allegation that it is not scientifically tested and proved to be efficient. This obligates those who believe in the treatment to seek it outside of the country and at the same time it brings a bad image for the Canadian Health System since it seems that it is not giving an opportunity of a better life to many Canadians.
I agree that in a public system that has shortage of resources we should avoid spending money with procedures unproven to be of any effect. But if there are evidences of positives effects then I think a good system would test the procedure on scientific grounds as soon as possible. But I would like to talk a little bit about the statistical part of this problem, one which the overall population is usually not aware of.
Suppose that 10 individuals with Multiple Sclerosis submit themselves to the new procedure under a non scientific environment (they just get the procedure without being in a controlled experiment) and one of them has some improvement. What usually happens is that there is a biased coverage of the 10 results by the media. 9 folks go home with no improvement and nobody talk about them while the one that had benefits becomes very happy and talk to everybody and the media interview the guy reporting perhaps that a new cure has been found. Now everybody with MS will watch the news and look for the procedure.
This is just one side of the absence of a designed scientific experiment. Others consequences at least as important are 1) the possibility that the improvement is just a short term one and things could even get worse after some time and 2) the possibility that we are looking at what is called placebo effect. Placebo Effect is the improvement in health conditions due to some reason other than the procedure. Sometimes just the fact that the somebody thinks he/she is receiving a miraculous treatment will cause some improvement.
We cannot say that the procedure is innocuous at the present moment. The right thing to do would be to conduct a controlled experiment as soon as possible so that if results are positive the maximum number of people can benefit from it. It is also important that the experiment be conducted in more than one place because only different instances with positive result can definitely validate the efficacy of the treatment. Fortunately it looks like trials have started in both US and Canada.
As for now it is quite hard to quantify the real effects of the treatment and we have to recognize that those who are facing MS have a difficult decision to make, even those who understand perfectly the possible inefficacy of this procedure. Without being able to assess the risks, should somebody with MS look for the treatment or wait until long lasting clinical trials results come along? I guess this will depend on the specific case, but it is a hard decision anyway....
Sunday, 12 September 2010
Friday, 10 September 2010
Respondent Driven Sampling
I just read this paper: Assessing Respondent-driven Sampling, published on the Proceedings of the National Academy of Sciences. The problem of measuring traits in rare population has always been a shortcoming of existing sampling method, when we think about practical applications.
I faced the challenge once, when I had to design a sample of homeless people in a very large city. But rather than talk about this specific work, I prefer to use it here as an example to show some problems we have with this type of challenge.
If you wanted to estimate the size of the homeless populations by means of a traditional sample, you would need to draw a quite large probabilistic sample to get some few homeless folks who will allow you to project results to the entire homeless population. The first problem with this is to make sure your sample frame cover the homeless population, because it will likely not. Usually samples that covers the human population of a country is ironically based on households (and we are talking about homeless people) and the nice fact the official institutes like Statistics Canada can give you household counts for small areas, which can then become units in your sample frame. Well, perhaps you can somehow include in your sample frame homeless people by looking for them in the selected areas and weighting afterwards... but I just want to make the point that we have already started with a difficult task even if we could draws a big probabilistic sample. Then I want to move on.
Usually estimating the size of rare population is only the least important of a list of goals a researcher has. The second goal would be to have a good sample of the targeted rare population so that we can draw inferences that are specific for that population. For example, we could be interested in the proportion of homeless people with some sort of mental disorder. This requires a large enough sample of homeless people.
One way to get a large sample of homeless people would be by referrals. It is fair to assume that the members of this specific rare population know other. Once we get one of them, they can indicate others in a process widely known as Snowball Sampling. Before the mentioned paper I was familiar with the term and just considered it as another type of Convenience Sampling for which inference always depends on strong assumption linked to the non probabilistic nature of the sample. But there are some literature on the subject and moreover, it seems to be more widely used than I thought.
Respondent Driven Sampling (RDS) seems to be the most modern way of reaching hidden populations. In a RDS an initial sample is selected and those sampled subjects receive incentive to bring their peers who also belongs to the given population hidden. They get incentives if they answer the survey and if they successfully bring others subjects. RDS would be different from the Snowball Sample because the later ask subjects to name their peers, not to bring them over to the research site. This is an interesting paper to learn more about it.
Other sampling methods include Targeted Sampling where the research tries to make a preliminary list of eligible subjects and sample from there. Of course this is usually not very helpful because of costs and again the difficulty to reach some rare population. Key Informant Sampling is a sample where you would select, for example, people that work with the target population. They would give you information about the population, that is, you would not really sample subjects from the population, but instead would make your inferences through secondary sources of information. Time Space Sampling (TTS) is method where you list places and within those places, times when the target population can be reach. For example, a list of public eating places could be used to find homeless people and you know what time they can be reach. It is possible to have valid inferences for the population that goes to these places by sampling places and times interval in this list. You can see more about TTS sampling and find other references in this paper.
Now to a point about the paper I first mentioned, how good is RDS Sampling? Unfortunately the paper does not brings good news. According to the simulations they did, the variability of the RDS sample is quite high, with median design effect around 10. That means a RDS sample of size n would be as efficient (if we think about Margin of Error) as a Simple Random Sample of size n/10. That makes me start questioning the research, although the authors make good and valid points defending the assumptions they need to make so that their simulations becomes comparable to a real RDS. I don't know, I cannot say anything, but I wonder if out there a survey exist that has used RDS sample for several consecutive waves. I think this kind of survey would give us some ideas of the variability involved on replications of the survey. Maybe we could look at some traits that are not expected to change from wave to wave and make an assessment of its variability.
An interesting property of the RDS is that it tends to lose it bias with time. For example, it was noticed that if a black person is asked for referrals, the referrals tend to be more black the actual proportion of black people in the population. This seems to me a natural thing in networks, I mean, people tend to have peers that are similar to themselves. This will happen with some (or maybe most) of the demographics characteristics. But it looks like the evident bias present in the first wave of referrals seemingly disappear around the sixth wave. That seems to me to be a good thing and if the initial sample cannot be random maybe we should consider disregarding waves 1 to 5 or so.
Anyway, I think as of today researches still face huge technical challenges when the target population is rare. RDS and other methods of reaching these populations have been developed which helps a lot, but this remains an unresolved issue for statistician, one very important in sampling methodology.
I faced the challenge once, when I had to design a sample of homeless people in a very large city. But rather than talk about this specific work, I prefer to use it here as an example to show some problems we have with this type of challenge.
If you wanted to estimate the size of the homeless populations by means of a traditional sample, you would need to draw a quite large probabilistic sample to get some few homeless folks who will allow you to project results to the entire homeless population. The first problem with this is to make sure your sample frame cover the homeless population, because it will likely not. Usually samples that covers the human population of a country is ironically based on households (and we are talking about homeless people) and the nice fact the official institutes like Statistics Canada can give you household counts for small areas, which can then become units in your sample frame. Well, perhaps you can somehow include in your sample frame homeless people by looking for them in the selected areas and weighting afterwards... but I just want to make the point that we have already started with a difficult task even if we could draws a big probabilistic sample. Then I want to move on.
Usually estimating the size of rare population is only the least important of a list of goals a researcher has. The second goal would be to have a good sample of the targeted rare population so that we can draw inferences that are specific for that population. For example, we could be interested in the proportion of homeless people with some sort of mental disorder. This requires a large enough sample of homeless people.
One way to get a large sample of homeless people would be by referrals. It is fair to assume that the members of this specific rare population know other. Once we get one of them, they can indicate others in a process widely known as Snowball Sampling. Before the mentioned paper I was familiar with the term and just considered it as another type of Convenience Sampling for which inference always depends on strong assumption linked to the non probabilistic nature of the sample. But there are some literature on the subject and moreover, it seems to be more widely used than I thought.
Respondent Driven Sampling (RDS) seems to be the most modern way of reaching hidden populations. In a RDS an initial sample is selected and those sampled subjects receive incentive to bring their peers who also belongs to the given population hidden. They get incentives if they answer the survey and if they successfully bring others subjects. RDS would be different from the Snowball Sample because the later ask subjects to name their peers, not to bring them over to the research site. This is an interesting paper to learn more about it.
Other sampling methods include Targeted Sampling where the research tries to make a preliminary list of eligible subjects and sample from there. Of course this is usually not very helpful because of costs and again the difficulty to reach some rare population. Key Informant Sampling is a sample where you would select, for example, people that work with the target population. They would give you information about the population, that is, you would not really sample subjects from the population, but instead would make your inferences through secondary sources of information. Time Space Sampling (TTS) is method where you list places and within those places, times when the target population can be reach. For example, a list of public eating places could be used to find homeless people and you know what time they can be reach. It is possible to have valid inferences for the population that goes to these places by sampling places and times interval in this list. You can see more about TTS sampling and find other references in this paper.
Now to a point about the paper I first mentioned, how good is RDS Sampling? Unfortunately the paper does not brings good news. According to the simulations they did, the variability of the RDS sample is quite high, with median design effect around 10. That means a RDS sample of size n would be as efficient (if we think about Margin of Error) as a Simple Random Sample of size n/10. That makes me start questioning the research, although the authors make good and valid points defending the assumptions they need to make so that their simulations becomes comparable to a real RDS. I don't know, I cannot say anything, but I wonder if out there a survey exist that has used RDS sample for several consecutive waves. I think this kind of survey would give us some ideas of the variability involved on replications of the survey. Maybe we could look at some traits that are not expected to change from wave to wave and make an assessment of its variability.
An interesting property of the RDS is that it tends to lose it bias with time. For example, it was noticed that if a black person is asked for referrals, the referrals tend to be more black the actual proportion of black people in the population. This seems to me a natural thing in networks, I mean, people tend to have peers that are similar to themselves. This will happen with some (or maybe most) of the demographics characteristics. But it looks like the evident bias present in the first wave of referrals seemingly disappear around the sixth wave. That seems to me to be a good thing and if the initial sample cannot be random maybe we should consider disregarding waves 1 to 5 or so.
Anyway, I think as of today researches still face huge technical challenges when the target population is rare. RDS and other methods of reaching these populations have been developed which helps a lot, but this remains an unresolved issue for statistician, one very important in sampling methodology.
Monday, 6 September 2010
Stepwise Regression
Never let the computer decide how your model should be. This is something I always try to stress in my daily work, meaning that we should include in our statistical models the knowledge that we have about the field we are working. The simplest example where we leave all decisions to the computer (or to the statistical program if you prefer) is when we run a stepwise regression.
Back in my school time it was just one of the ways we had to do variable selection in a regression model, when we had many variables. I did not consult the literature but my feeling is that by then people just were not aware of the problems of stepwise regression. Nowadays if you try to defend Stepwise Regression in a table with statisticians they will shoot you down.
It is not difficult to find papers discussion the problems of Stepwise. We have two examples here and here. I think one of the problems with Stepwise selection is the one I said above, it take out of the hands of the researcher the responsibility of thinking - the computer decides what should be in the model, what should not, using criteria not aways understood by those who runs the model. Another problems is the overfitting or capitalization on chance. Stepwise is often used when there are many variables and these are precisely the cases where you will easily have some variables in just by chance.
I ran a quick simulation on this. I generated a random dependent variables and 100 random independent variables and went on to run a stepwise regression using the random variables to explain the dependent variable. Of course we should not find any association here, all the variables are independent random variables. The histogram below show the R-square of the resulting model. If the sample size is 300 the R-Square will explain between 10% and 35% of the variability in Y. If the sample size is larger, say 1000 cases, then the effect of Stepwise is less misleading as the higher sample size protects against overfitting.
The overfitting is easily seem in Discriminant Analysis as well, which also has variable selection options.
There are at least two ways of avoiding this type of overfitting. One would be to include random variables in the data file and stop the stepwise whenever a random variable is selected. The other is to run the variable selection in a subset of the data file and validate the result using the rest. Unfortunately none of these procedures are easy to apply since current softwares does not allow you to stop the Stepwise when variable X enter the model and usually the sample size is too small to allow for a validation set.
Depending on the nature of the variable an interesting approach could be to run an exploratory Factor Analysis or Principal Component Analysis and include all the factors in the model.
Hopefully Stepwise Regression will be used with more caution if used at all. Below you have the SAS code I used to generate the simulations for these two histograms. I am not very good SAS programmer, I am sure someone can write this in a more elegant way... Sorry I did nto have time to insert comments...
%macro step;
%do step=1 %to &niter;
%put &step;
data randt;
array x[&nind] x1 - x&nind;
do i = 1 to &ncases;
y=rand('UNIFORM');
do j = 1 to &nind;
x[j] = rand('UNIFORM');
end;
output;
end;
run;
proc reg data = randt outest = est edf noprint;
model y = x1 - x&nind/selection = stepwise adjrsq;
run;
%if &step > 1 %then %do;
data comb;
set comb est;
run;
%end;
%else %do;
data comb;
set est;
run;
%end;
%end;
%mend step;
%let nind = 100;
%let ncases = 1000;
%let niter = 200;
%step;
Back in my school time it was just one of the ways we had to do variable selection in a regression model, when we had many variables. I did not consult the literature but my feeling is that by then people just were not aware of the problems of stepwise regression. Nowadays if you try to defend Stepwise Regression in a table with statisticians they will shoot you down.
It is not difficult to find papers discussion the problems of Stepwise. We have two examples here and here. I think one of the problems with Stepwise selection is the one I said above, it take out of the hands of the researcher the responsibility of thinking - the computer decides what should be in the model, what should not, using criteria not aways understood by those who runs the model. Another problems is the overfitting or capitalization on chance. Stepwise is often used when there are many variables and these are precisely the cases where you will easily have some variables in just by chance.
 |
| R-Square for 200 simulations where 100 random variables explain a dependent variable in a dataset with 1000 units. |
The overfitting is easily seem in Discriminant Analysis as well, which also has variable selection options.
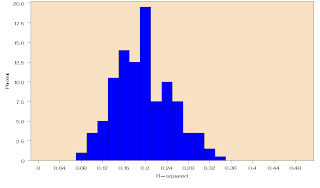 |
| R-Square for 200 simulations where 100 random variables explain a dependent variable in a data set of 300 units. |
Depending on the nature of the variable an interesting approach could be to run an exploratory Factor Analysis or Principal Component Analysis and include all the factors in the model.
Hopefully Stepwise Regression will be used with more caution if used at all. Below you have the SAS code I used to generate the simulations for these two histograms. I am not very good SAS programmer, I am sure someone can write this in a more elegant way... Sorry I did nto have time to insert comments...
%macro step;
%do step=1 %to &niter;
%put &step;
data randt;
array x[&nind] x1 - x&nind;
do i = 1 to &ncases;
y=rand('UNIFORM');
do j = 1 to &nind;
x[j] = rand('UNIFORM');
end;
output;
end;
run;
proc reg data = randt outest = est edf noprint;
model y = x1 - x&nind/selection = stepwise adjrsq;
run;
%if &step > 1 %then %do;
data comb;
set comb est;
run;
%end;
%else %do;
data comb;
set est;
run;
%end;
%end;
%mend step;
%let nind = 100;
%let ncases = 1000;
%let niter = 200;
%step;
proc univariate data=Work.Comb noprint;
var _RSQ_;
histogram / caxes=BLACK cframe=CXF7E1C2 waxis= 1 cbarline=BLACK cfill=BLUE pfill=SOLID vscale=percent hminor=0 vminor=0 name='HIST' midpoints = 0 to 0.5 by 0.01;
run;
Saturday, 4 September 2010
The "Little Jiffy" rule and Factor Analysis
Factor Analysis is a statistical technique we use all the time in Marketing Research. It is often the case that we want to uncover the dimensions in the consumer's mind that can help to explain variables of interest like Overall Satisfaction and Loyalty. Questionnaire are often cluttered with a whole bunch of attributes that makes the understanding of the analysis difficult and tiresome. To make matters worse it is not uncommon to see people wanting to run Regression Analysis with 20 or 30 attributes highly correlated. I don't want to talk about Regression here, but to me the only way out in these cases is to run a Factor Analysis and work with factors instead.
Back in my university years I learnt that Factor Analysis had to be rotated with Varimax Rotation, especially if you wanted to use the factor as independent variables in a Regression Analysis because this way the factors would have the optimum property of being orthogonal and their effects could be estimated purely in a Regression Analysis. Using the Varimax Rotation along with Principal Component Analysis and retaining as many factor as there are eigenvalues higher than 1 in the correlation matrix is the so called "Little Jiffy" approach for factor analysis. And it is widespread, you not only learn it in the school, you will see people using it all the time and you will find lots of papers following the approach. I remember this one from a research I did while doing some analyses for a paper.
In the workplace I soon noticed that you pay a price for having beautifully orthogonal factors to use in your regression: they are not always easy to be interpreted and even when the factors make sense they are not so sharply defined as one would like. It also makes more sense not to constrain factors to be independent because we have no evidence that if these factors exist in real world they are orthogonal. So I abandoned the orthogonal rotation.
The number of factors to retain is something more subtle. I think the eigenvalue higher than 1 rule usually gives a good starting point for the Exploratory Factor Analysis, but I like to look at several solutions and choose the one easier to interpret as the factor has to be understood as it will be target for actions on the client side.
Finally I want to link to this paper, which is an interesting source for those who works with Factor Analysis. There is something in the example (with measures of boxes...) that I don't like, maybe the non linear dependence of some measure on others would tell us that we should not expect Factor Analysis to perform well. It would be better to simulate data clearly following a certain factor model structure and explore it instead.
Do not let the computer decide what to do with the data, by using the Little Jiffy rule of thumb, instead take a more proactive approach and bring your knowledge in, don't be afraid to think your problem and what makes more sense in your specific situation.
Back in my university years I learnt that Factor Analysis had to be rotated with Varimax Rotation, especially if you wanted to use the factor as independent variables in a Regression Analysis because this way the factors would have the optimum property of being orthogonal and their effects could be estimated purely in a Regression Analysis. Using the Varimax Rotation along with Principal Component Analysis and retaining as many factor as there are eigenvalues higher than 1 in the correlation matrix is the so called "Little Jiffy" approach for factor analysis. And it is widespread, you not only learn it in the school, you will see people using it all the time and you will find lots of papers following the approach. I remember this one from a research I did while doing some analyses for a paper.
In the workplace I soon noticed that you pay a price for having beautifully orthogonal factors to use in your regression: they are not always easy to be interpreted and even when the factors make sense they are not so sharply defined as one would like. It also makes more sense not to constrain factors to be independent because we have no evidence that if these factors exist in real world they are orthogonal. So I abandoned the orthogonal rotation.
The number of factors to retain is something more subtle. I think the eigenvalue higher than 1 rule usually gives a good starting point for the Exploratory Factor Analysis, but I like to look at several solutions and choose the one easier to interpret as the factor has to be understood as it will be target for actions on the client side.
Finally I want to link to this paper, which is an interesting source for those who works with Factor Analysis. There is something in the example (with measures of boxes...) that I don't like, maybe the non linear dependence of some measure on others would tell us that we should not expect Factor Analysis to perform well. It would be better to simulate data clearly following a certain factor model structure and explore it instead.
Do not let the computer decide what to do with the data, by using the Little Jiffy rule of thumb, instead take a more proactive approach and bring your knowledge in, don't be afraid to think your problem and what makes more sense in your specific situation.
Subscribe to:
Comments (Atom)